Vektoren

Notation

$$ \vec{v} = \begin{pmatrix} v_x \ v_y \ v_z \end{pmatrix} $$

Vektoren werden immer klein geschrieben und Punkte groß geschrieben.

Betrag Eines Vektors (Länge)

$$ |\vec{v}|= \sqrt{{v_x}^2 + {v_y}^2 + {v_z}^2} $$

Skalare Multiplikation Und Division

Bei der Multiplikation eines Vektors mit einem Skalar verändert sich die Länge des Vektors. Die Division funktioniert gleich.

$$ \vec{v} \cdot a = \begin{pmatrix} v_x \cdot a \ v_y \cdot a \ v_z \cdot a \end{pmatrix} $$

Gegenvektor / Inverse

Bei der Multiplikation eines Vektors mit -1 erhält man den entgegengesetzten Vektor, auch inverser Vektor genannt.

$$ - \vec{v} $$

Vektoren Addieren Und Subtrahieren

Addition

Bei dem Addieren von Vektoren ensteht ein Vektor, der Anfangspunkt und Endpunkt verbindet.

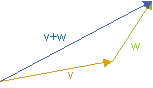
$$ \vec{v} + \vec{w} = \begin{pmatrix} v_x + w_x \ v_y + w_y \ v_z + w_z \end{pmatrix} $$

Subtraktion

Bei der Subtraktion von Vektoren erhält man den Vektor, der die Länge zwischen zwei Vektoren ausmacht. Der Vektor verbindet die beiden Vektoren, betrachtet als Ortsvektoren.

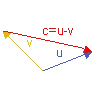
$$ \vec{u} - \vec{v} = \begin{pmatrix} u_x - v_x \ u_y - v_y \ u_z - v_z \end{pmatrix} $$

Das Gleiche funktioniert mit zwei Punkten aus, denen ein Vektor entsteht, der von Anfangspunkt zu Endpunkt zeigt. Dies nennt man Translation.

$$ Endpunkt - Anfangspunkt $$

$$ \overrightarrow{AE} = \begin{pmatrix} E_x - A_x \ E_y - A_y \ E_z - A_z \end{pmatrix} $$

Ortsvektor

Der Ortsvektor ist ein Vektor, der den Koordinatenursprung als Anfangspunkt hat. Er beschreibt die Position eines Punktes im Verhältnis zu diesem Ursprung.

$$ \vec{v} = \overrightarrow{OP} = \begin{pmatrix} P_x \ P_y \ P_z \end{pmatrix} $$

Der Punkt O ist der Ursprung des Koordinatensystems, in der Regel $(0,0,0)$, und P ein beliebiger Punkt.

Bei einer Geraden wird der Ortsvektor auch Aufpunkt genannt.

Einheitsvektor

Kanonischen Einheitsvektoren

Der Einheitsvektor ist ein Vektor, der eine Länge von 1 hat. Es gibt 3 Standard-Einheitsvektoren, die im 3-dimensionalen Raum für die Achsen verwendet werden.

$$ \vec{e}_1 = \begin{pmatrix} 1 \ 0 \ 0 \end{pmatrix} \newline \vec{e}_2 = \begin{pmatrix} 0 \ 1 \ 0 \end{pmatrix} \newline \vec{e}_3 = \begin{pmatrix} 0 \ 0 \ 1 \end{pmatrix} $$

Normieren

Beim Normieren eines Vektors, wird seine Länge auf 1 geändert, indem man ihn durch seinen Betrag teilt. Das Resultat ist der Einheitsvektor.

$$ \vec{e}_{\vec{v}} = \frac{\vec{v}}{|\vec{v}|} $$

Skalarprodukt

Das Skalarprodukt ist eine mathematische Methode zur Messung der Ähnlichkeit zwischen zwei Vektoren. Es wird als Innerer Winkel bezeichnet und berechnet sich wie folgt:

$$ \vec{v} \cdot \vec{w} = |\vec{v}| \cdot |\vec{w}| \cdot \cos(\theta) $$

wobei $\theta$ der Winkel zwischen den beiden Vektoren ist.

Winkel Berechnen

Um den inneren Winkel zu berechnen muss man die Formel auf $\theta$ umstellen.

$$ \theta = \arccos(\frac{\vec{v} \cdot \vec{w}}{|\vec{v}| \cdot |\vec{w}|}) $$

Kreuzprodukt Zweier Vektoren (T. S. 74)

$$ \vec{v} \times \vec{w} = \begin{pmatrix}v_y w_z - v_z w_y \ v_z w_x - v_x w_z \ v_x w_y - v_y w_x\end{pmatrix} $$

Die Länge / der Betrag des Kreuzproduktes $\vec{a} \times \vec{b}$ ist gleich der Fläche des Parallelogramms, das von a und b aufgespannt wird.

Orthogonaler Vektor

Zwei Vektoren die senkrecht zueinander stehen sind orthogonale Vektoren. Das Skalarprodukt zweier orthogonaler Vektoren ist immer 0.

Kollinieare Vektoren

Kollinear bedeutet, dass zwei Vektoren in derselben Richtung verlaufen. Die Länge der Vektoren müssen dabei nicht übereinstimmen.

Richtungsvektor

Der Richtungsvektor einer Geraden gibt an, in welche Richtung sie verläuft und ist immer orthogonal zur Geraden. Ein Richtungsvektor kann berechnet werden, indem man zwei Punkte, Anfangspunkt und den Endpunkt, der Geraden betrachtet und die Ortsvektoren subtrahiert.

Vektorgleichungen

Geraden

Geradengleichung

$$ \vec{g} = \overrightarrow{OP} + \lambda \vec{r} $$

Die Gleichung besteht aus dem Aufpunkt und einem mit Lambda multiplizierten Richtungvektor.

Punkte Auf Geraden

Ein Punkt auf einer Geraden ist ein Aufpunkt. Ein Punkt liegt dann auf einer Geraden, wenn das Lambda für alle Komonenten gleich ist.

Bei dem Berechnen von Lambda setzt man den Vektor $\vec{g}$ mit dem Ortsvektor $\overrightarrow{OP}$ des gegebenen Punktes gleich.

Beziehungen Zwischen Geraden

Parallel

Zwei Vektorgleichungen sind parallel, wenn der Richtungsvektor der einen gleich dem Richtungsvektor der anderen ist. Wenn die Richtungsvektoren verschieden sind, können die Geraden schneiden oder windschief sein.

• Richtungsvektoren normieren
• Wenn sie gleich oder invers sind, dann sind sie parallel

Schnitt

Um herauszufinden, ob sich zwei Geraden schneiden, muss man die Parametergleichungen beider Geraden gleich setzen und nach Lambda aufgelöst werden. Wenn das Ergebnis eine eindeutige Lösung hat, schneiden sich die beiden Geraden. Wenn das Ergebnis keine eindeutige Lösung hat, sind die Geraden parallel.

Wir betrachten die folgenden zwei Vektorgleichungen:

$$ \vec{g_1} = \overrightarrow{OA} + \lambda \cdot \vec{r_1} $$

$$ \vec{g_2} = \overrightarrow{OB} + \mu \cdot \vec{r_2} $$

Gleichungen gleichsetzen und mihilfe des LGS (Gleichungen komponentenweise austellen) nach Lambda oder Mu auflösen:

$$ \overrightarrow{OA} + \lambda \cdot \vec{r_1}_x = \overrightarrow{OB} + \mu \cdot \vec{r_2}_x \newline \overrightarrow{OA} + \lambda \cdot \vec{r_1}_y = \overrightarrow{OB} + \mu \cdot \vec{r_2}_y \newline \overrightarrow{OA} + \lambda \cdot \vec{r_1}_z = \overrightarrow{OB} + \mu \cdot \vec{r_2}_z $$

Windschief

Geraden werden als windschief bezeichnet, wenn sie sich weder schneiden noch parallel zueinander sind. Windschiefe Geraden gibt es nur ab dem R³.

Abstand Zwischen Punkt Und Gerade

• Vektor bliden der Orthogonal ist (Skalarprodukt 0)
• Vektorgleichung bilden (mit Punkt und orthogonalen Vektor)
• Schnittpunkt finden
• Abstand zwischen Schnittpunkt und Punkt berechnen

Ebenen

Punkt Auf Ebene

3 Punkte (die nicht auf einer Gerade liegen) liegen immer in einer Ebene.

Ebenen:

$$ \overrightarrow{OA}+\lambda_1 \cdot \overrightarrow{AB} + \lambda_2 \cdot \overrightarrow{AC} $$

gegeben: Ebenengleichung und Koordinaten eines Punktes

gesucht: Liegt der Punkt auf der Ebene?

Lösungsverfahren:

Prüfe, ob der Punkt zur Menge der Ebenenpunkte gehört. Setze den Ortsvektor gleich mit der Ebenengleichung → komponentenweise auflösen (LGS) → auflösen nach lambda 1 und lambda 2 → mit der nicht benutzten Gleichung überprüfen.

Der Normalenvektor

Der Normalenvektor ist ein Vektor, der senkrecht auf etwas anderem Steht. Das kann eine Gerade, Ebene oder theoretisch auch eine gekrümmte Linie sein.

Normalenvektor einer Ebene

Bei einer Ebene in Parameterform ist der Normalenvektor das Kreuzprodukt der beiden Richtungsvektoren: $$ \vec{N} = \vec{r_1} \times \vec{r_2} $$ Bei einer Ebene in Koordinatenform bildet sich der Normalenvektor aus den Koeffizienten a, b und c:

Ebene: $ax+by+cz=d$ $\begin{pmatrix} a \ b \ c \end{pmatrix}$= ist der Normalenvektor der Ebene, also orthogonal zur Ebene

Normalenvektor einer Geraden

Bei einer Geraden im R³ gibt es unendlich viele Normalenvektoren. Diese lassen sich mittels des gleich null gesetzten Skalarprodukts berechnen.

Bei einer Geraden im R²

Koordinatenform

$$ ax+by+cz=d $$ In der Koordinatenform sind a, b und c die Komponenten des Normalenvektors.

Ebenenscharen

Eine Ebenenschar ist eine Menge von Ebenen, die sich alle durch eine gemeinsame Gleichung beschreiben lassen, die einen zusätzlichen freien Parameter a enthält.

Lage Zwischen Ebene Und Gerade

Möglichkeiten

• Gerade schneidet die Ebene → gemeinsamer Punkt
• Gerade liegt in der Ebene → alle (unendlich viele) Punkte
• Gerade schneidet die Ebene nicht → 0 Punkte gemeinsam

Schnittpunkt

1. Ebene in Koordinatenform bringen, falls nicht bereits gegeben
2. Gerade komponentenweise in Ebene einsetzen und auf Unbekannte auflösen.
3. Ergebnis in die Geradengleichung einsetzen.

Lage Zwischen Ebenen

Möglichkeiten

• Ebenen schneiden sich → gemeinsame Schnittgerade
• Ebenen liegen ineinander → all (unendlich viele) Punkte
• Ebenen sind prallel und liegen nicht ineinander → 0 Punkte gemeinsame

Schnittgerade

1. Eine Ebene in Koordinatenform und die andere Ebene in Parameterform bringen.
2. Komponentenweise die Parameterform in die Koordinatenform einsetzen.
3. Auf eine Unbekannte auflösen.
4. Ergebnis in die Parameterform einsetzen und zusammenfassen (zusammenfassen durch komponentenweises Aufschreiben und anschließendes Zurückwandeln vereinfachen)

Typische Aufgaben Der Linearen Algebra Und Lösungsverfahren

1. Geradengleichung aus 2 Punkten aufstellen

   • Wandle Punkte in Ortsvektoren um
   • Bilde die Differenz der beiden Ortsvektoren → Richtungsvektor der Geraden
   • Wähle einen der beiden gegebenen Punkte als Aufpunkt

2. Prüfe, ob ein Punkt auf einer Geraden liegt

   • Wandle den Punkt in einen Ortsvektor um
   • Setze den Ortsvektor mit der Geradengleichung gleich
   • Schreibe die Geradengleichung dann Komonentenweise hin → LGS mit 1 Unbekannten
   • Löse eine der Gleichungen nach Lambda auf
   • Setze Lambda in alle anderen Gleichungen ein, und prüfe ob diese erfüllt sind. Wenn ja liegt der Punkt auf der Gerade.

3. Schneiden sich zwei Geraden? (g und h)

   • Setze die Vektor-Geradengleichungen gleich
   • Schreibe die Geradengleichung komponentenweise hin → LGS mit 2 Unbekannten (ggf. aus 3 Gleichungen)
   • Löse das Gleichungssystem (du erhältst Lambda 1 und Lambda 2)
   • Sollte das LGS nicht lösbar sein oder unendlich viele Lösungen besitzen, dann schneiden sich die Geraden nicht
   • Nur im R³: Setze Lambda 1 / 2 in die noch nicht benutzte Gleichung ein. Nur wenn diese erfüllt ist, dann schneiden sich die Geraden

   Hinweis: in R³ gibt es die zusätzliche Lagebeziehung “windschief”.