Differentialrechnung
Differentialrechnung
ℝ = Reelle Zahlen x∈ℝ = x ist eine Reelle Zahl s.m.w. = streng monoton wachsend s.m.f. = streng monoton fallend
Intervall: x∈ℝ, x∈ [0, 1] Alle Zahlen zwischen 0 und 1. Geschlossenes Intervall Umgedrehtes A bedeutet (∀): für alle x∈(0, 1) Alle Zahlen < 1 und > 0. Offenes Intervall Sei f(x) eine Funktion a, b ∈ ℝ; a < b; x ∈ [a, b] dann heißt f(x) auf [a, b] streng monoton wachsend, genau dann wenn (g.d.w.) ∀x1, 2 ∈ [a, b] und x1 < x2 f(x1) < f(x2)
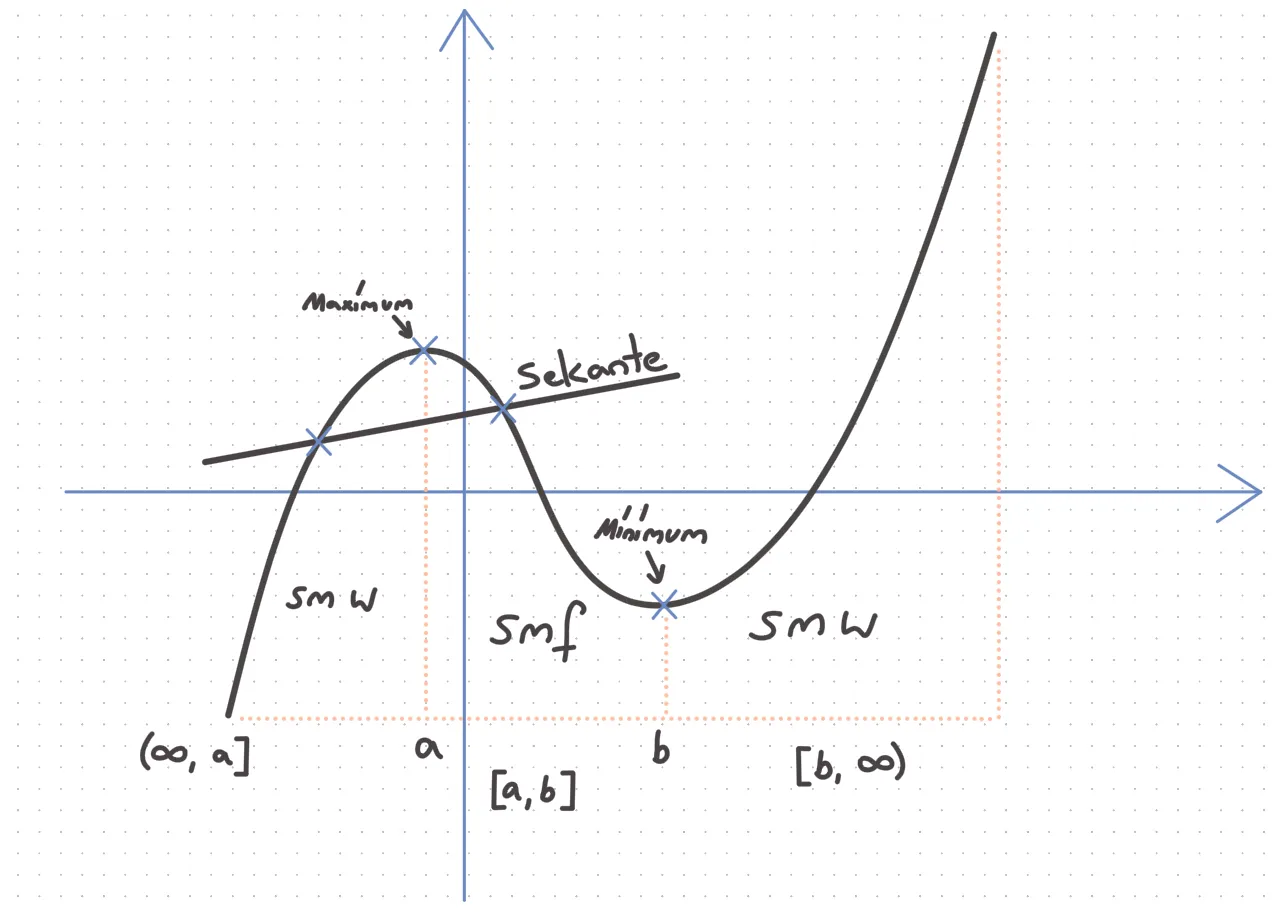
Sei f(x) eine Funktion auf ℝ dann heißt a∈ℝ ein Maximum von f(x)
b∈ℝ ein Minimum von f(x)
g.d.w. x<a f(x) s.m.w. x>a f(x) s.m.f. xb s.m.b
An Extremstellen (und nur da) ändert sich das Monotonieverhalten! Was ist eine Nullstelle? 0 = f(x) g.d.w. Sei f(x) eine Funktion auf ℝ dann heißt x0 ∈ ℝ NS von f(x) g.d.w. f(x0) = 0
| Zeichen | Bezeichnung | Beispiel | Gegenbeispiel |
|---|---|---|---|
| ℕ | natürliche Zahlen | 1; 5 | -1; Pi; $\frac{1}{3}$ |
| ℤ | ganze Zahlen | -1; 4 | 1,5; ; $- \frac{1}{3}$ |
| ℚ | rationale Zahlen | $\frac{1}{3}$ | Pi; ± |
| ℝ | reelle Zahlen | 1; Pi; ; $- \frac{1}{3}$ | i ( ) |
Definitionsbereich und Wertebereich einer Funktion: $f(x)\ = \ \frac{1}{x}$ Definitionsbereich = x ∈ ℝ ∩ x ≠ 0 Wertebereich = f(X) ∈ ℝ ∩ f(X)≠ 0 ∩ = und; ∪ = oder Definitionsbereich = Alle Werte, die X sein dürfen Wertebereich = Alle Werte, die bei f(x) herauskommen. Eine Funktion heißt stetig g.d.w. sie mit einem Strich gezeichnet werden kann, ohne abzusetzen. Beispiel: x²; Gegenbeispiel: 1/x
Sekantenanstieg: Betrachte s(t) = 2t² + 4t
- skizziere die Funktion - Check
- Bestimme die Durchschnittsgeschw.
Intervalle: zw. t∈[0, 1] = Ø 6 s/t t∈[-1, 3] = Ø 8 s/t t∈[0, 2] = Ø 8 s/t Durschnittsgeschw. (Ø) = $\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ bzw. $\frac{\text{Δy}}{\text{Δx}}$ Durchschnittliche / Mittlere Geschwindigkeit zwischen Punkten ⇔ Anstieg der Gerade, die durch die 2 Punkte führt! Die Gerade schneidet die Funktion in 2 Punkten. Analog zum Kreis heißt die Gerade dann (auch) Sekante. Wir haben also den Sekantenanstieg berechnet!!
- mittlere Änderungsrate
- durchschnittliche Änderungsrate
Beispiel 2: $f(x) = \frac{1}{2}x^{4} + 3x - 2$ x∈[0, 1] = x∈[-2, 2] = x∈[-1/4, 4] = $y1 = - \frac{1407}{512}\ y2 = 138$ == 31,824 = -0,3849602 Beispiel 3: f(x) = 10x² + 3 g(x) = log10(x)
| X0 | Y1 | Anstieg f(x) | Anstieg g(x) |
|---|---|---|---|
| 1 | 2 | 30 | 0.301 |
| 1 | $\frac{3}{2}$ | 25 | 0.352 |
| 1 | $\frac{1001}{1000}$ | 20.01 | 0.434 |
| 2 | 3 | 50 | 0.176 |
| 2 | 2.5 | 45 | 0.194 |
| 2 | 2.01 | 40.1 | 0.217 |
| 1 | 0.99 | 19.9 | 0.436 |
Von der durchschnittlichen zur momentanen Änderungsrate - Die Anstiegsfunktion Anstieg einer Funktion an einer Stelle (ein Punkt):
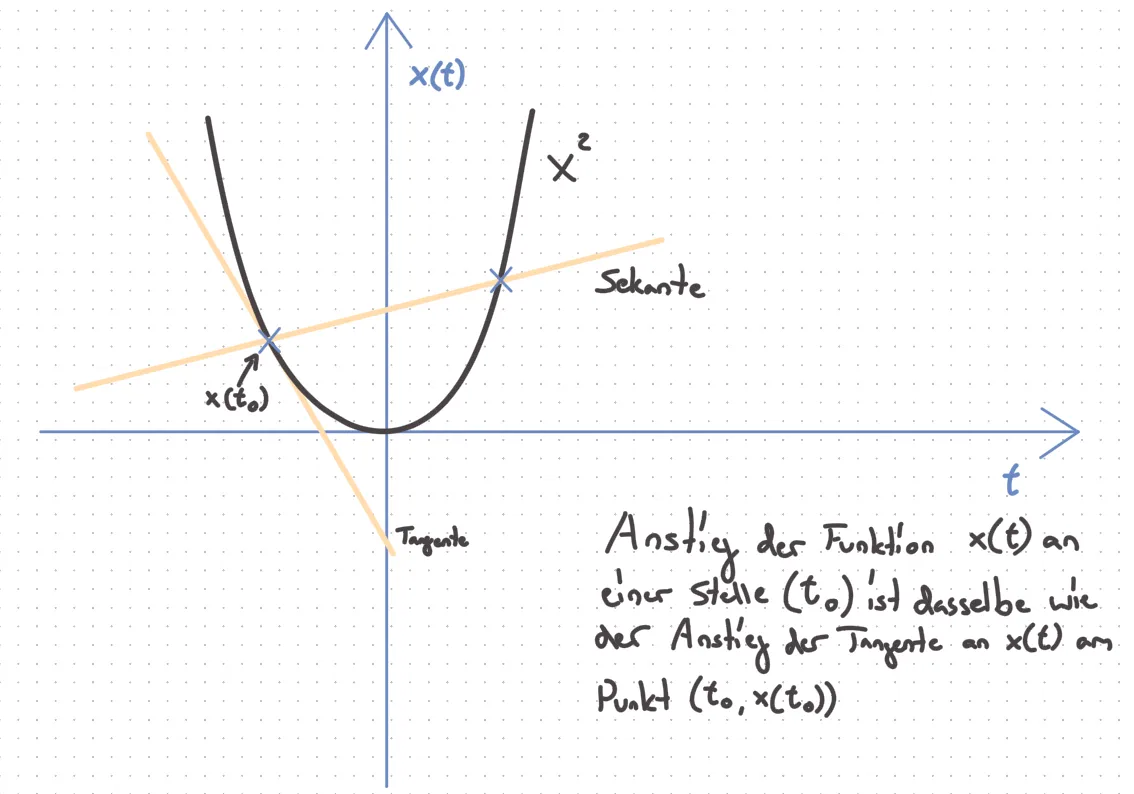
Funktionen, bei denen man die Tangente nicht eindeutig bestimmen kann, heißen (an diesen Stellen) nicht differenzierbar. An der Stelle p(0|0) der Funktion f(x)=|x| ist sie nicht differenzierbar. Anstiegsfunktion: Anstiege an allen x-Stellen: x → Anstieg von f (x) f ’ (x) 1. Ableitung von f(x), beschreibt den Anstieg von f (x) bei allen x∈ⅅ⊂ℝ
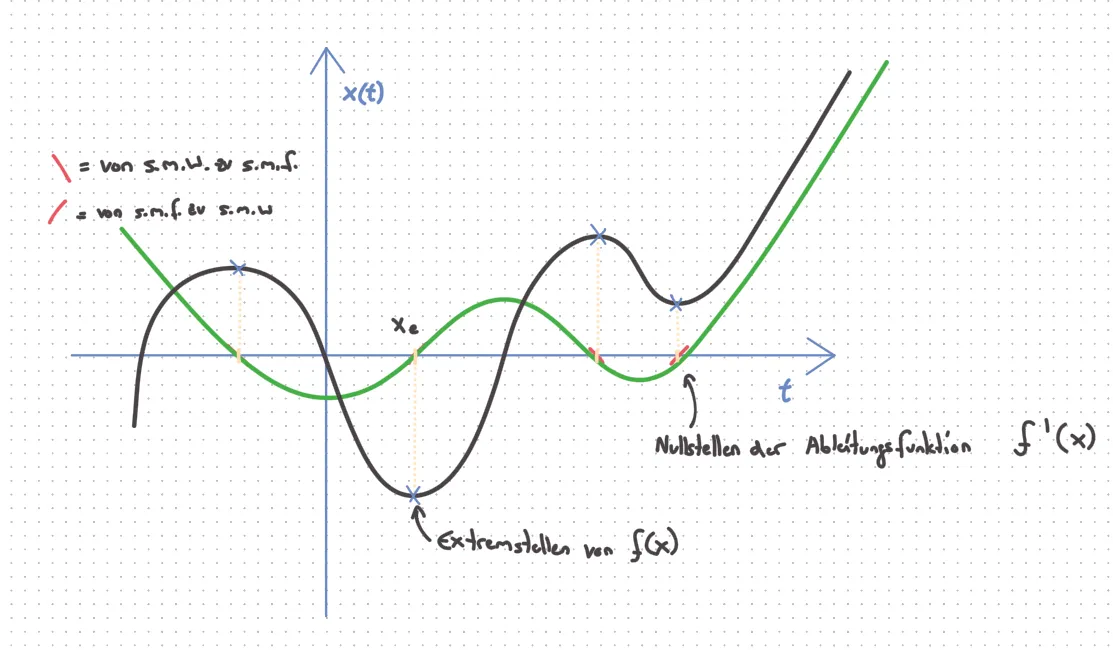
Ableitung = lokaler Anstieg = Tangentensteigung = momentane Änderungsrate s (t) ’ = v (t) s ’’ (t) = v(t)’ = a (t) Zum Zusammenhang zwischen f(x) und f ‘ (x): f ‘ (x) beschreibt den Anstieg der Funktion f(x) (Tangentenanstieg = 1 Punkt, wo der Anstieg berechnet wird). Extremstellen von f(x) sind Nullstellen von f ‘ (x). f ‘ (XE) = 0 (XE = Extremstelle) Skizziere die Ableitung zu: f(x) = (x+3)*(x-4)*x g(x) = sin(x) h(x) = sin(x)/x sei f ‘ (x) = 2x skizziere f(x) g ‘ (x) = -2x² skizziere g(x) sin(x) ‘ = cos(x) Wie berechnet man die Änderungsrate? x1 − x0 = h x1 = x0 + h f(x) = f(x0 + h) − f(x0) $m = \frac{f(x_{0} + h) - f(x_{0})}{h}$o Grenzwertprozess: limes h->0 Sekantenanstieg = Tangentenanstieg $m = \frac{f(x_{0} + h) - f(x_{0})}{h}$ limes h − > 0
- Schreibe die Funktionswerte für x0 und x0+h
- vereinfache
- “setze” h=0
- Das Ergebnis ist der Tangentenanstieg bei X0
Beispiel: f(x) = x² x0 = 2 gesucht: f ′ (x0) 1. $\frac{\text{limes}}{h - > 0}\ \frac{f(x_{0} + h) - f(x_{0})}{h}$ einsetzen: $\frac{\text{limes}}{h - > 0}\ \frac{f(2 + h) - f(2)}{h}$ $\frac{\text{limes}}{h - > 0}\ \frac{(2 + h)² - 2²}{h}$ 2. umformen: $\frac{\text{limes}}{h - > 0}\ \frac{4 + 4h + h² - 4}{h} = \frac{4h + h²}{h}$ $= \frac{4h + h²}{h}\ |/h$ $\frac{\text{limes}}{h - > 0}\ 4 + h = 4$ f(x) = 4 + 2x * x3 Ableitungsfunktionen bestimmen ohne lim h→0 Methode:
- Regel:
Von f (x) = x² ist die Ableitungsfunktion: f ‘ (x) = 2x
- Regel:
Von f (x) = xn ist die Ableitungsfunktion: f ‘ (x) = n*xn-1
HIER:
f(x) = sin(x2)
f′(x) = cos(x2) * 2x
$f(x) = \frac{x}{x^{2} - 1} = x*{(x - 1)}^{- 2}$
f(x) = − 2(x − 1) − 3
$\frac{n}{x^{e}} = n*x^{- e}$
$\frac{n}{x^{e}} = nx^{- e}$
https://www.youtube.com/watch?v=fK9SRATRbDQ
KETTENREGEL:
f(x) = u(v(x))
f′(x) = u′(v(x)) * v′(x)
Ganzrationale Funktionen / Polynome:
| Funktionstyp | f(x) | f ‘ (x) |
|---|---|---|
| Konstante | f(x)=a oder z.B. f(x)=42 | f ‘ (x) = 0ax0-1= 0 |
| lineare Funktion | f(x)=mx+b | f ‘ (x) = m |
| Polynom | f(x)=xn oder z.B. f(x)=x4 | n*xn-1 |
| Summe: | f (x) = u (x) + v (x) f (x) = 5 + x7 | f ‘ (x) = u ‘ (x) + v ’ (x) f ‘ (x) = 0 + 7 * x7-1 | | --- | --- | --- | | Produkt: | f (x) = 𝛼 * u (x) f (x) = 3 * x² | f (x) = 𝛼 * u ‘ (x) f ‘ (x) = 3*2x1 = 6x |
Konstante Faktoren bleiben erhalten. Konstanten in einer Summe verschwinden. Die Ableitung der Summe ist die Summe der Ableitungen der Einzelfunktionen.
$s(t) = \frac{1}{2}10t² + 3t + 1$
s ′ (t) = 10t + 3
$f(x) = \frac{1}{2}(x + 1)(x - 2)$
$f(x) = \frac{1}{2}2x - \frac{1}{2}$
Der Punkt einer Funktion, bei dem sich das Krümmungsverhalten ändert, heißt Wendepunkt.
Das Krümmungsverhalten ist entweder rechts oder links gekrümmt. Links gekrümmt, wenn sich die funktion auf dem Graphen von -x nach +x nach links dreht, dann ist die links gekrümmt.
- Parabel, Konstante
- x³ und x5
- sin(x) mit dem Intervall [-4, 2]
| Grad (maximaler Exponent) | EP (Extrempunkt) | WP (Wendepunkt) | NS (Nullstelle, maximal möglich) | | --- | --- | --- | --- | | 0 | 0 | 0 | 0 | | 1 | 0 | 0 | 1 | | 2 | 1 | 0 | 2 | | 3 | 2 | 1 | 3 | | n | n-1 | n-2 | n |
$\sqrt[n]{x^{e}} = x^{\frac{e}{n}}$
ab * ac = ab + c
$\frac{n}{x^{e}} = nx^{- e}$
f(x) = u(v(x))
f′(x) = u′(v(x)) * v′(x)
f(x) = 3x + (2x + x2)10
f′(x) = 3 + 10 * (2x + x2)9 * (2 + 2x)
